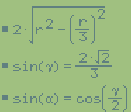
Con γ è indicato l'angolo ottuso in C, con α l'angolo in A.
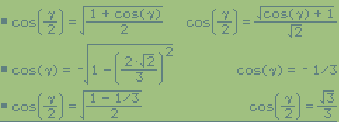
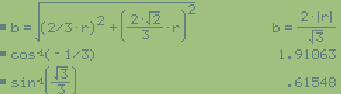
Perciò il perimetro:
f(x)=4Ö(2)r/3+2r·sin(x)+2r·sin(θ+x) essendo x variabile tra 0 (quando PºA) e π–cos-1(1/3) @ 1.91063 (quando PºB)
Ovvero, applicando una delle formule di prostaferesi:
f(x)=4Ö(2)r/3+2r·2sin(x+θ/2)cos(θ/2)
Quindi, poiché cos(θ/2)=Ö((1+cos(θ))/2)=Ö(2/3), si ottiene:
f(x)/(2r)=2Ö(2)/3(1+Ö(3)·sin(x+cos-1(1/3)/2)).
